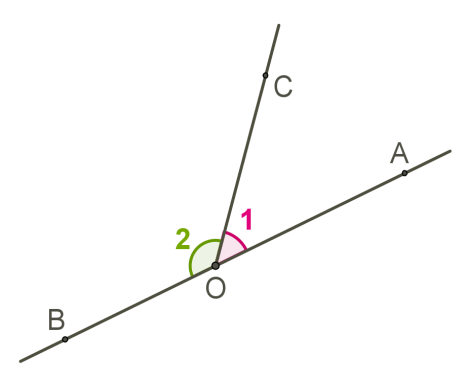
Суміжними називаються два кути, одна сторона яких спільна, а дві інші утворюють пряму, тобто є доповняльними променями.
Властивості:
Властивості:
Сума суміжних кутів дорівнює 180 градусам.
Два суміжних кути утворюють розгорнутий кут.
Якщо два кути рівні, то суміжні з ними кути теж рівні.
Кут, суміжний із прямим кутом, є прямим.
Кут, суміжний з гострим кутом, є тупим.
Кут, суміжний з тупим кутом, є гострим.
Будь-який промінь, що виходить із вершини розгорнутого кута і проходить між його сторонами, поділяє його на два суміжні кути.
Якщо два кути рівні, то суміжні з ними кути також рівні.
Два кути, суміжні з одним і тим же кутом, рівні.
Якщо два суміжні кути рівні, то вони прямі.
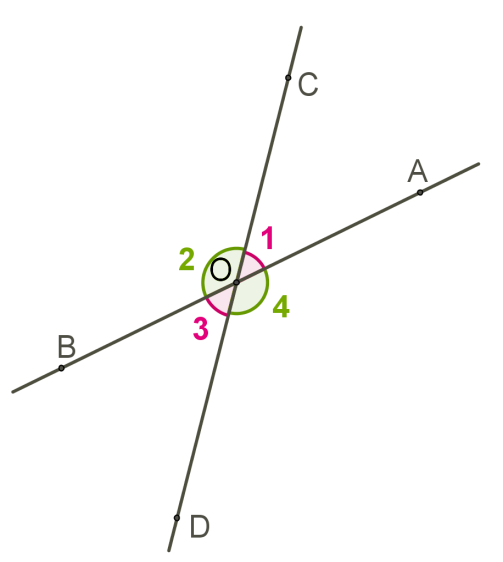
Вертикальними називаються два кути, сторони одного з яких є доповняльними променями до сторін другого кута.
Властивості:
Вертикальні кути рівні.
Два суміжних кути утворюють розгорнутий кут.
Якщо два кути рівні, то суміжні з ними кути теж рівні.
Кут, суміжний із прямим кутом, є прямим.
Кут, суміжний з гострим кутом, є тупим.
Кут, суміжний з тупим кутом, є гострим.
Будь-який промінь, що виходить із вершини розгорнутого кута і проходить між його сторонами, поділяє його на два суміжні кути.
Якщо два кути рівні, то суміжні з ними кути також рівні.
Два кути, суміжні з одним і тим же кутом, рівні.
Якщо два суміжні кути рівні, то вони прямі.
Вертикальними називаються два кути, сторони одного з яких є доповняльними променями до сторін другого кута.
Властивості:
Вертикальні кути рівні.
При перетині двох прямих утворюються дві пари вертикальних кутів (2 гострих і 2 тупих; або 4 прямих, якщо прямі паралельні) і чотири пари суміжних кутів.
Якщо відомий один із кутів, що утворились при перетині двох прямих, то знайти інші кути можна таким чином: знайти кут, суміжний з даним, враховуючи, що їх сума 180 градусів, після чого знайти кути, вертикальні з відомими, враховуючи, що вертикальні кути рівні.
Тренувальні вправи:
1. Один з кутів, що утворюються при перетині двох прямих, у 4 рази більший за інший. Знайти ці кути.
2. Знайти суміжні кути, якщо один з них на 38⁰ більший за другий.
3. Знайти величину кожного з кутів, які утворюються при перетині двох прямих, якщо сума двох з них дорівнює 98⁰.
4. Який кут утворює бісектриса кута 48⁰ з продовженням одніїє з його сторін з аершину?
5. Різниця між двома суміжними кутами дорівнює меншому з них. Знайти ці кути.
2. Знайти суміжні кути, якщо один з них на 38⁰ більший за другий.
3. Знайти величину кожного з кутів, які утворюються при перетині двох прямих, якщо сума двох з них дорівнює 98⁰.
4. Який кут утворює бісектриса кута 48⁰ з продовженням одніїє з його сторін з аершину?
5. Різниця між двома суміжними кутами дорівнює меншому з них. Знайти ці кути.
Запам’ятайте поняття про теорему, аксіому та доведення.
Доведення — міркування про правильність твердження про властивість тієї або іншої геометричної фігури.
Теорема — твердження, яке треба довести.
Аксіома — твердження, що не потребують доведення, і які містяться у формулюваннях основних властивостей найпростіших фігур.
Доведення — міркування про правильність твердження про властивість тієї або іншої геометричної фігури.
Теорема — твердження, яке треба довести.
Аксіома — твердження, що не потребують доведення, і які містяться у формулюваннях основних властивостей найпростіших фігур.

Немає коментарів:
Дописати коментар