Алгоритм для малювання тессеракта - чотиривимірного куба

Почну з пояснення, що ж таке чотиривимірний простір.

Це - одновимірний простір, тобто просто вісь OX. 

Будь-яка точка на ній характеризується однією координатою.

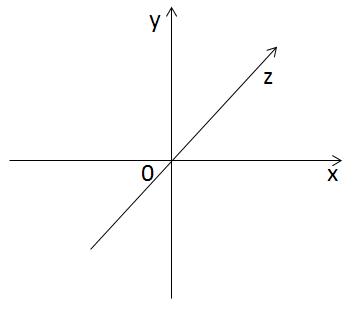
Тепер проведемо вісь OY перпендикулярно осі OX. Ось і є двовимірний простір, тобто площина XOY. Будь-яка точка на ній характеризується двома координатами - абсцисою і ординатою.

Проведемо вісь OZ перпендикулярно осям OX та OY. Вийде тривимірний простір, в якому у будь-якої точки є абсциса, ордината і аппліката.

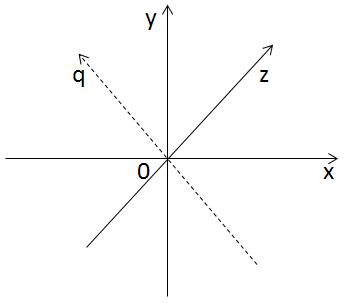
Логічно, що четверта вісь, OQ, повинна бути перпендикулярна осям OX, OY і OZ одночасно. Але ми не можемо точно побудувати таку вісь, і тому залишається тільки спробувати уявити її собі. У кожної точки в чотиривимірному просторі є чотири координати: x, y, z і q.

Тепер подивимося, як з'явився чотиривимірний куб.

На картинці зображено фігура одновимірного простору - лінія.
Якщо зробити паралельне перенесення цієї лінії уздовж осі OY, а потім з'єднати відповідні кінці двох одержаних ліній, вийде квадрат.

  
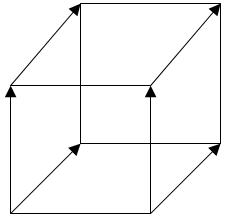
Аналогічно, якщо зробити паралельне перенесення квадрата уздовж осі OZ і з'єднати відповідні вершини, то вийде куб.

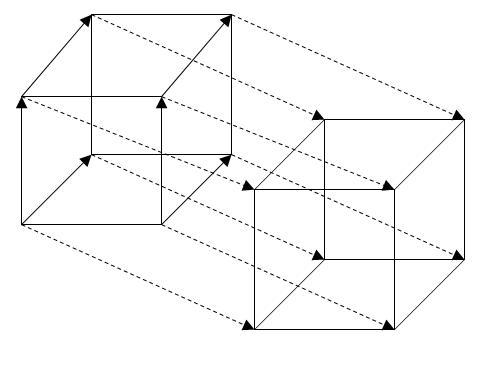
А якщо зробити паралельне перенесення куба вздовж осі OQ і з'єднати вершини двох цих кубів, то ми отримаємо чотиривимірний куб. До речі, він називається тессеракт.

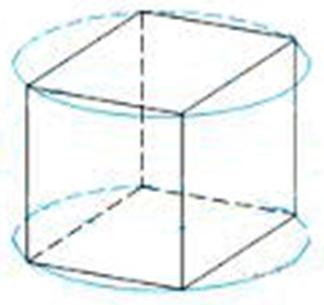
Щоб намалювати куб на площині, потрібно його спроектувати. Наочно це виглядає так:

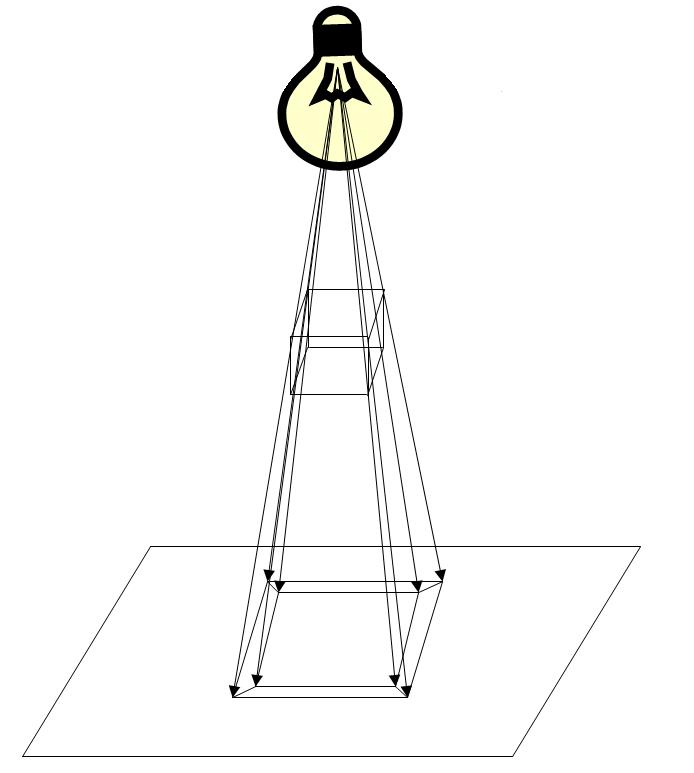
Уявімо, що в повітрі над поверхнею висить каркасна модель куба, тобто як би «зроблена з дроту», а над нею - лампочка. Якщо включити лампочку, обвести олівцем тінь від куба, а потім вимкнути лампочку, то на поверхні буде зображена проекція куба.

Перейдемо до більш складного. Ще раз подивіться на малюнок з лампочкою: як бачите, все промені зійшлися в одній точці. Вона називається точкою сходження і використовується для побудови перспективної проекції (А буває і паралельна проекція, коли всі промені паралельні один одному. Результат - НЕ створюється відчуття об'єму, і при тому якщо точка сходження досить сильно віддалена від проектованого об'єкта, то різниця між цими двома проекціями мало помітна). Щоб спроектувати дану точку на дану площину, використовуючи точку сходження, потрібно провести пряму через точку сходження і дану точку, а потім знайти точку перетину отриманої прямої і площини. А для того, щоб спроектувати більш складну фігуру, скажімо, куб, потрібно спроектувати кожну його вершину, а потім відповідні точки з'єднати. Слід зауважити, що алгоритм проекції простору на підпростір можна узагальнити для випадку 4D -> 3D, а не тільки 3D -> 2D.

Ми не можемо собі точно уявити, як виглядає вісь OQ, так само як і тессеракт. Зате ми можемо отримати обмежене уявлення про нього, якщо ми спроектуємо його на об'єм, а потім намалюємо це на екрані комп'ютера!

Тепер поговоримо про проекції Тессеракта.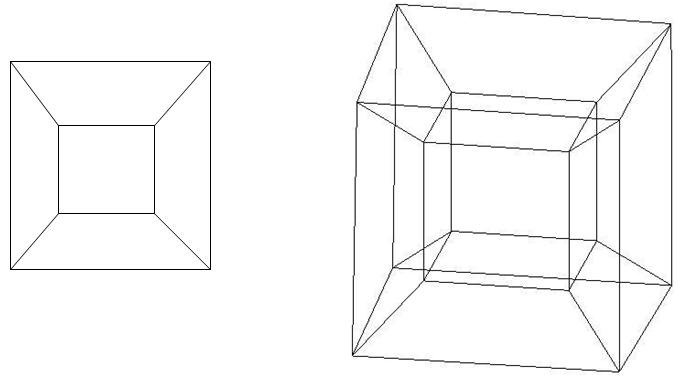
Зліва знаходиться проекція куба на площину, а праворуч - Тессеракт на простір. Вони досить схожі: проекція куба виглядає як два квадрата, маленький і великий, один всередині іншого, і у яких відповідні вершини з'єднані лініями. А проекція Тессеракта виглядає як два куба, маленький і великий, один всередині іншого, і у яких відповідні вершини з'єднані. Але ми всі бачили куб, і можемо з упевненістю сказати, що і маленький квадрат, і великий, і чотири трапеції зверху, знизу, праворуч і ліворуч від маленького квадрата, насправді є квадратами, при чому рівними. І у Тессеракта теж саме. І великий куб, і маленький куб, і шість усічених пірамід з боків від маленького куба - це все куби, при чому рівні.

Ця програма вміє не тільки малювати проекцію Тессеракта на простір, а ще й обертати його. Розглянемо, як це робиться.

Для початку я вам розповім, що таке обертання паралельно площині.

Уявіть собі, що куб обертається навколо осі OZ. Тоді кожна з його вершин описує коло навколо осі OZ.

А коло - фігура плоска. І площини кожного з цих кіл паралельні між собою, і в даному випадку паралельні площині XOY. Тобто ми можемо говорити не тільки про обертання навколо осі OZ, а ще й про обертання паралельно площині XOY.

 Як бачимо, у точок, які обертаються паралельно осі XOY змінюються тільки абсциса і ордината, аппліката ж залишається незмінною. І, взагалі-то, ми можемо говорити про обертання навколо прямої тільки тоді, коли маємо справу з тривимірним простором. У двовимірному все обертається навколо точки, в чотиривимірному - навколо площини, в пятивимірному просторі ми говоримо про обертання навколо простору. І якщо обертання навколо точки ми можемо собі уявити, то обертання навколо площині і простору - щось немислиме. А якщо будемо говорити про обертання паралельно площині, то тоді в будь-якому n-вимірному просторі точка може обертатися паралельно площині.

Багато з вас, ймовірно, чули про матрицю повороту. Помноживши точку на неї, отримаємо точку, повернену паралельно площині на кут фі... 

...Для того, щоб спроектувати точку тривимірного простору на площину, просто розглянемо дві площини - XOZ і YOZ, і для кожної з них вирішимо це завдання. У разі чотиривимірного простору потрібно розглянути вже три площини: XOQ, YOQ і ZOQ.

І нарешті, про програму. Вона діє так: форматувати шістнадцять вершин Тессеракт -> в залежності від введених користувачем команд повернути його -> спроектувати на простір -> в залежності від введених користувачем команд повернути його проекцію -> спроектувати на площину -> намалювати.

Архів з програмою і інструкцією користування: www.dropbox.com/s/xilxouqmgnsf6zs/%D0%A2%D0%B5%D1%81%D1%81%D0%B5%D1%80%D0%B0%D0% BA% D1% 82.rar (потрібно завантажити і встановити програму Dropbox: www.dropbox.com)

Исходник: docs.google.com/document/d/1sGjBTb-od84Qp_la0LS9tWFZL4aYk-1exUs0Za5_Uq0/edit

 3,4,5,6-мірний куб. Як будуються багатовимірні фігури, в простих словах