Геометрія 7 кл. Кути, утворені при перетині двох прямих січною. Паралельні прямі і січна

Аксіома паралельних прямих:
Через точку, що не лежить на даній прямій, можна провести пряму,
паралельну даній, і до того ж тільки одну.

Пряма, яка перетинає дві задані прямі, називається січною цих прямих.

При перетині прямих січною утворюються такі пари кутів:

• кути, що лежать між прямими і по один бік від січної, називаються внутрішніми односторонніми кутами; маємо дві пари внутрішніх односторонніх кутів;
• кути, що лежать між прямими і по різні боки від січної, називаються внутрішніми різносторонніми кутами; маємо дві пари внутрішніх різносторонніх кутів; 
• кути, що лежать по один бік від січної, але один із них лежить між заданими прямими, а інший не лежить між ними, називаються відповідними; маємо чотири пари відповідних кутів. 

Ознака паралельності прямих:

Якщо при перетині двох прямих січною внутрішні різносторонні кути рівні або сума внутрішніх односторонніх кутів дорівнює 180 градусам, то задані прямі паралельні.

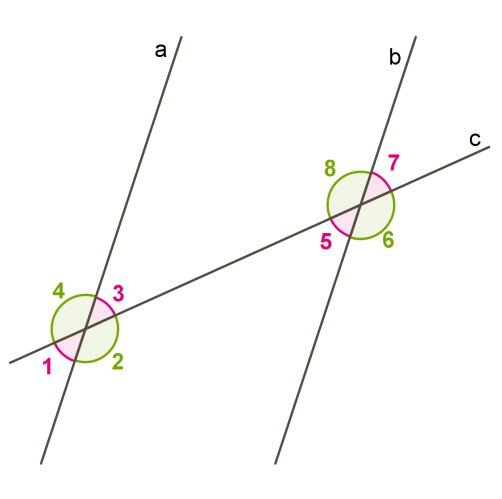  При перетині двох паралельних прямих третьою січною:

• внутрішні різносторонні кути рівні ( ∠3 =∠5, ∠2 =∠8);
• відповідні кути рівні (∠1=∠3=∠5=∠7 і ∠2=∠4=∠6=∠8);
• сума внутрішніх односторонніх кутів дорівнює 180° (∠2+∠5=180°, ∠3+∠8=180°). 

Наслідки ознаки паралельності прямих:

• Дві прямі, перпендикулярні до третьої, паралельні між собою.
• Прямі є паралельними, якщо при їх перетині січною утворені відповідні кути рівні, внутрішні різносторонні кути рівні; сума двох внутрішніх односторонніх кутів  дорівнює 180 градусам.

Зверніть увагу! Якщо пряма перпендикулярна одній паралельній прямій, то вона перпендикулярна й інший.