Квадрат суми двох чисел дорівнює квадрату першого числа плюс
подвоєний добуток першого числа на друге і плюс квадрат другого числа.
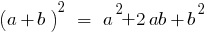
Квадрат різниці двох чисел дорівнює квадрату першого числа мінус подвоєний добуток першого числа на друге і плюс квадрат другого числа.
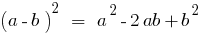
Різниця квадратів двох чисел дорівнює добутку суми цих чисел на їх різницю.
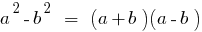
Куб суми двох чисел дорівнює кубові першого числа плюс потроєний добуток квадрат першого числа на друге, плюс потроєний добуток першого числа на квадрат другого і плюс куб другого числа.
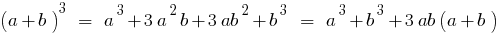
Куб різниці дорівнює кубові першого числа мінус потроєний добуток квадрата першого числа на друге, плюс потроєний добуток першого числа на квадрат другого і мінус куб другого числа.
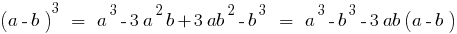
Сума кубів двох чисел дорівнює добуткові суми цих чисел на неповний квадрат різниці цих чисел.
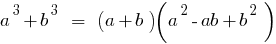
Різниця кубів двох чисел дорівнює добуткові різниці цих чисел на неповний квадрат суми цих чисел.
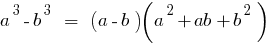
Квадрат суми кількох виразів дорівнює сумі квадратів усіх доданків плюс усі подвоєні добутки кожного виразу на кожний наступний.
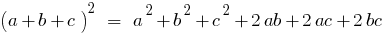
Правила розкриття дужок:
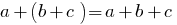
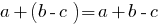
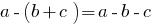
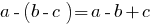
1. Множення одночлена на многочлен 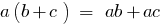
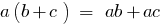
2. Множення многочлена на многочлен 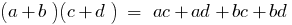
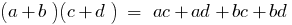
3. Винесення спільного многочлена за дужки 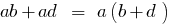
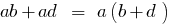
4. Метод групування 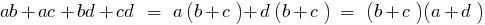
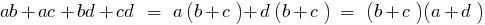
5. Виділення квадрата двочлена з квадратного тричлена
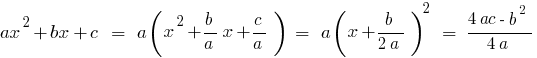
1. Для виразів 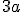 і
і 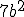 запишіть:
запишіть:
а) квадрат різниці; в) куб різниці;
б) різницю квадратів; г) різницю кубів.
2. Піднесіть до квадрата:
a)^2) ; б)
; б) ^2) ; в)
; в) ^2) .
.
а) квадрат різниці; в) куб різниці;
б) різницю квадратів; г) різницю кубів.
2. Піднесіть до квадрата:
a)
3. Розв'яжіть рівняння ^2=56+x^2) .
.
4. Спростіть вираз: ^2-(7a-b)(7a+b)) .
.
5. Доведіть тотожність: ^2+10(2a^n+3)-(a^n+5)^2=30.)
6. Знайти число, протилежне до кореня рівняння:
^2-5(y-6)(y+6)=2(18-y^2).)
7. Обчислити 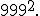
ТРЕНУВАЛЬНІ ВПРАВИ:
1. Спростіть вираз:
a)^2;) b)
b) ^2;) c)
c) ^2-70ab;) d)
d) ^2-64a^2.)
2. Спростіть вираз:
a)^2+y(y-7);) b)
b) +(4-a)^2;) c)
c) ^2-2x(6-x)^2;) d)
d) %20\cdot%20c%20-(1-c)^2.)
3. Спростіть вираз:
a)(3b+1);) b)
b) (5b-6);) c)
c) \left%20(%207+\frac{1}{2}a%20\right%20).)
4. Спростіть вираз:
a)(a-2b);) b)
b) (3x+y);) c)
c) (5c-2a).)
5. Спростіть вираз:
a)(x+y)(x^2+y^2);) b)
b) (4a^2+b^2)(2a-b);) c)
c) (c^3-b)(c^6+b^2);)
d)(3m+2)+4;) e)
e) (7-5n);) f)
f) (x+0,5).)
6) Розв'яжіть рівняння:
a)^2-x(x+8)=2;) b)
b) -(3y+1)^2=1;)
c)-(x-5)^2=2;) d)
d) +(4x-5)^2=0.)
1. Спростіть вираз:
a)
2. Спростіть вираз:
a)
3. Спростіть вираз:
a)
4. Спростіть вираз:
a)
5. Спростіть вираз:
a)
d)
6) Розв'яжіть рівняння:
a)
c)
Розв'язання 1.
а)^2) ; б)
; б) ^2-(7b^2)^2) ; в)
; в) ^3) ; г)
; г) ^3-(7b^2)^3) .
.
Розв'язання 2
a)^2=a^2+2am+m^2) ; б)
; б) ^2=81b^2-36b+4) ;
;
а)
Розв'язання 2
a)
в) ^2=\frac{1}{25}x^2+2x+25) .
.
Розв'язання 3.
Розв'язання 3.
Застосуємо формулу "квадрат двочлена"для розкриття дужок.
Розв'язання 4.
Доведення 5. Спростимо ліву частину тотожності, застосувавши формули скороченого множення "квадрат різниці двох виразів" і "квадрат суми двох виразів" та розкриття дужок, а потім зведемо подібні доданки.
Розв'язання 6. Розкриємо дужки, застосувавши формули скороченого множення.
^2-5(y-6)(y+6)=2(18-y^2);%20\\%203y^2-12y+12-5y^2+180=36-2y^2;%20\\3y^2-12y-5y^2+2y^2=36-180-12;%20\\%20%20-12y=-156;%20\\%20y=13.)
Відповідь. -13.
Розв'язання 7.
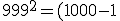^2=1000^2-2%20\cdot%201000%20\cdot%201%20+1^2=1000000-2000+1=998001.)
Відповідь. -13.
Розв'язання 7.

Немає коментарів:
Дописати коментар