ПЕРВІСНА, ЇЇ ЗАСТОСУВАННЯ

І. ПЕРВІСНА до функції. ТАБЛИЦЯ ПЕРВІСНИХ. 

 

ПРАВИЛА ЗНАХОДЖЕННЯ ПЕРВІСНИХ.

1. Означення первісної.

Функцію F(х) називають первісною для функції f(x) на заданому проміжку, якщо для всіх х з цього проміжку F'(х) = f(х).

Приклад. Для функції f(х) = 2х на інтервалі (-∞;+∞) первісною є функція F(х) = х², оскільки кожного х з цього інтервалу виконується рівність 

2. Основна властивість первісних.

Повертаючись до прикладу попереднього пункта, можна зауважити, що наприклад функція F₁(х) = х² + 1 має ту саму похідну, що й функція F(х) = х², дійсно (х² + 1)’ = 2х. Тому функція F₁(х) = х²+ 1 є також первісною для функції f(х) = 2х. Зрозуміло, що замість числа 1 можна поставити будь-яке інше число С, та матимемо (х² +C)’ = 2х.

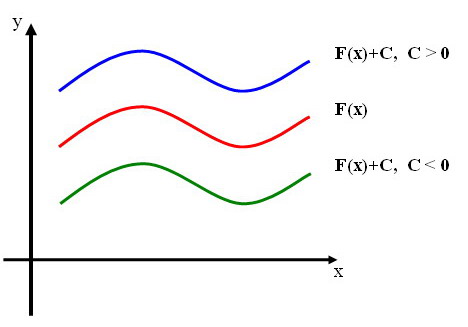
Приходимо до основної властивості первісної: кожна з первісних для функції f(x) на заданому проміжку має вигляд F(х) + С, де F(х) - одна з цих первісних, а С - довжина стала.

 

Графіки будь-яких первісних одержуються один з одного паралельним перенесенням уздовж осі ОУ.

3. Таблиця первісних.

Для знаходження первісних деяких функцій, корисною є таблиця первісних(невизначених інтегралів).

Функція f(x)	Загальний вигляд первісних F(х)+С , де С - довільна стала
0	С
1	х + С
xα, α ≠ -1
1/x	ln|х| + С
sin x	-соs х + С
cos x	sіn х + С
1/cos2 x	tg х + С
1/sin2 x	-ctg x + С
ex	ех + С
ax (a > 0; a ≠ 1)

Розглянемо приклади.

Приклад 1. Знайдіть усі первісні для функції:

Розв’язання. Використаємо те, що загальний вигляд первісних для функції x^α має вигляд 

2) Оскільки

3) Оскільки

4) Маємо

Приклад 2. Для функції f(х) = sіn х знайдіть первісну, графік якоїпроходить через точку 

Розв’язання. Загальний вигляд первісних для функції f(х) = sіn х такий F(х) = -соs х + С.

За умовою графік шуканої первісної проходить через точку  Тому підставляємо π/3 замість х, а -1(1/2) замість F(х) у загальний вигляд первісної, матимемо

Отже, шукана первісна F₁(x) = - cos х - 1.

4. Правила знаходження первісних(невизначених інтегралів).

1) Якщо F - первісна для f, a G - первісна для g, то F + G - первісна для f + g.

2) Якщо F - первісна для f, а k - стала, то kF - первісна для kf.

3) Нехай F(x) - первісна для f(х), a k і b - деякі сталі, причому k ≠ 0. Тоді 1/k ∙ F(kx + b) - первісна для функції f(kx + b).

Розглянемо приклади використання цих правил.

Приклад 1. Знайдіть загальний вигляд первісних для функцій:

Розв’язання.

1) Оскільки х⁵/5 первісна для х⁴, a tg x - первісна для 1/cos² x, то використовуючи правило 1, матимемо загальний вигляд первісних для заданої функції:

2) Оскільки е^х - первісна для е^х, то використовуючи правило 2, матимемо загальний вигляд первісних для заданої функції F(х) = 7е^х + С.

Приклад 2. Знайдіть загальний вигляд первісних для функції 

Розв’язання. Для соs х однією з первісних є sin х. Використовуючи правило 3, матимемо загальний вигляд первісних для заданої функції:

Приклад 3. Для функції  знайдіть первісну F(x) таку,що F(12) = 3.

Розв’язання. Використовуючи правило 3 та той факт, що однією з первісних для функції х⁵ є x⁶/6 матимемо:

Оскільки F(12) = 3, то матимемо 

Отже,  - шукана первісна.

Приклади знаходження невизначених інтегралів:

ІІ. ВИЗНАЧЕНИЙ ІНТЕГРАЛ. 

ФОРМУЛА НЬЮТОНА-ЛЕЙБНІЦА.

Визначеним інтегралом від неперервної на [а;b] функції f(x) з нижньою межею а і верхньою межею b називають різницею F(b) -F(a), де F(x) - одна з первинних для функції f(x).

 Позначають визначений інтеграл так f(x)dx.

При обчисленні різниці F(b) - F(а) можна брати будь-яку з первісних функцій f(х), що записуються в загальному вигляді F(x) + С. Але прийнято застосовувати ту первісну для якої С = 0.

За наведеним означенням маємо:

Цю формулу називають формулою Ньютона-Лейбніца:

Розглянемо приклади знаходження визначених інтегралів.

Приклад 1. Обчисліть інтеграл sіn хdх.

Розв’язання. Для функції f(х) = sin х однією з первісних є F(х) = -cos х. Маємо за формулою Ньютона-Лейбніца

Приклад 2. Обчисліть інтеграл 

Розв’язання. Спочатку знайдемо первісну для функції f(х) = 2х +3х² + 1. Використовуючи правила обчислення первісних та таблицю первісних, маємо:

Матимемо

Зауважимо, що при оформленні цього прикладу знаходження первісної можна було не записувати окремо. Тоді оформлення набуде наступного вигляду:

Приклад 3. Обчисліть інтеграл 

Розв’язання. Використаємо правило 3 знаходження первісних. Маємо

ІІІ. ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА ДО ОБЧИСЛЕННЯ ПЛОЩ КРИВОЛІНІЙНИХ ТРАПЕЦІЙ, ПЛОЩ ПЛОСКИХ ФІГУР ТА ПРИКЛАДНИХ ЗАДАЧ.

1. Означення криволінійної трапеції та знаходження її площі.

Нехай на відрізку [а;b] осі абсцис задано неперервну функцію у = f(x), яка на цьому відрізку набуває лише тільки невід’ємні значення. Фігуру, обмежену графіком функції у = =f(х), віссю абсцис та прямими х = а, х = b називають криволінійною трапецією (мал. 113). Її площу S можна знайти за допомогою визначеного інтеграла

Приклад 1. Обчисліть площу криволінійної трапеції, обчисленої графіком функції f(х) = х³ та прямими у = 0; х = 1; х = 2.

Розв’язання (мал. 114). Маємо

Приклад 2. Обчисліть площу криволінійної трапеції обмеженої графіком функції f(x) = sin х та прямими 

Розв’язання (мал. 115). Маємо

2. Обчислення площ плоских фігур. 

Розглянемо площу фігур зверху обмежену графіком функцій у = /(х), знизу - графіком функції у = f(х) та вертикальними прямими х = а і х = b, причому функції у = f(x) і у = g(х) - неперервні на [а;b] і для всіх значень х  [а;b] виконується нерівність f(x) ≥ g(x) (мал. 116). Тоді площу S такої плоскої фігури можна знайти за формулою:

Приклад 1. Знайдіть площу фігури, обмежену графіками функцій у = соs х, у = -2 соs х та прямими x = 0 i x = π/6.

Розв’язання (мал. 117). Маємо

Підінтегральний вираз можна спростити. Отримаємо

Приклад 2. Знайдіть площу фігури, обмежену графіками функцій у = х² - 2х і у = 4х + х.

Розв’язання. Знайдемо абсциси точок перетину графіків функцій:х² - 2х = 4 + х; х² - 3х - 4 = 0; x₁ = -1; x₂ = 4.

Ординати точок перетину y₁ = 3; у₂ = 8. Зображуємо графіки функцій схематично (мал. 118).

Шукана площа

3. Обчислення об’єму тіла обертання.

Нехай криволінійна трапеція, обмежена графіком неперервної на [а;b] функції у = f(x), такою що f(х) ≥ 0 для кожного х  [а;b] та прямими у = 0; х = а; х = b, обертається навколо осі абсцис (мал. 119). Тоді об’єм утвореного тіла обертання можна знайти за формулою:

Приклад. Знайдіть об’єм тіла, отриманого обмеженням навколо осі абсцис криволінійної трапеції, обмеженої лініями у = ; у = 0; x = 1; x = 4.

Розв’язання. Криволінійна трапеція, що обертається подана на малюнку 120. Об’єм утвореного тіла

4. Переміщення матеріальної точки, що рухається прямолінійно.

Нехай матеріальна точка рухається прямолінійно зі швидкістю, що в кожний момент часу визначається за формулою υ = υ(t). Тоді за проміжок часу шлях S, який пройшла точка, визначається формулою:

Приклад. Матеріальна точка рухається прямолінійно з швидкістюυ(t) = 4 + 0,8t (м/с). Знайдіть шлях, який пройде точка за проміжок часу від t₁ = 10с до t₂ = 20 с.

Розв’язання. Маємо

5. Робота сили, що діє на матеріальну точку.

Нехай матеріальна точка рухається вздовж осі абсцис під дією сили, проекція якої на цю вісь - неперервана на [а;b] функція f(x). І нехай під дією цієї сили матеріальна точка переміщується з точки М(а) в точку N(b). Тоді роботу А цієї сили можна обчислити за формулою:

Приклад. Обчисліть роботу сили F при розтягу пружини на 0,1 м, якщо при розтягу пружини на 0,02 м потрібна сила 6Н.

Розв’язання. За законом Гука, сила F пропорційна розтягу (або стиску) пружини, тобто F = kх, де х - величина розтягу або стиску,k-постійна.

Оскільки при х = 0,02 м маємо F = 6Н, то можна знайти коефіцієнт  Отже F = 300x. Роботу А по розтягу пружини на 0,1 м знайдемо так

КОНТРОЛЬНИЙ ТЕСТ № 6.

 1. Знайти загальний вигляд первісної для функції: 

2. Для функції f(х) = соs х знайдіть первісну, графік якої проходить через точку А(π/2;-2).

3. Знайти загальний вигляд первісних для функції: 

4. Знайти загальний вигляд первісної для функції: 

5. Для функції f(х) = е^2х-1 знайти таку первісну F(x), що F(0,5) = 3.

6. Обчислити інтеграл: х³dх.

7. Обчислити інтеграл: 

8. Обчислити площу криволінійної трапеції, обмеженої 

графіком функції у = х² та прямими у = 0, х = 0, х = 6.

9. Знайти площу фігури, обмежену графіками функцій у = 2 sіn х, 

у = -sіn х та прямими x = 0, x = π/3.

10. Знайти об’єм тіла, отриманого обертанням навколо осі абсцис криволінійної трапеції, обмеженої лініями у = , у = 0, х = 1, х= 4.

11. Обчислити інтеграл 

12. Знайти площу фігури, обмежену лініями у = 3 - х² і у = 1 - х.