Приклади задач з розв'язками
№1. Навколо правильної трикутної піраміди описано конус. Знайти площу бічної поверхні конуса, якщо сторона основи піраміди дорівнює
Розв’язання.
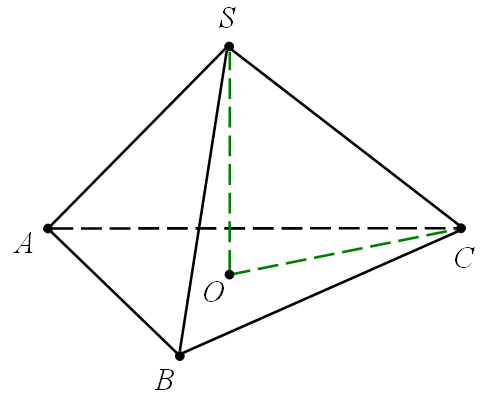
Зауваження. Для розв’язання задачі малювати конус немає потреби: достатньо розглянути піраміду.
Нехай навколко піраміди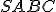 описано конус. За умовою
описано конус. За умовою 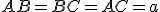 ,
, 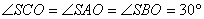 ,
, 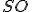 –висота піраміди.
–висота піраміди.
Оскільки всі ребра піраміди рівно нахилені до площини основи, то
точка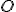 є центром описаного кола навколо
є центром описаного кола навколо 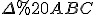 , тобто
, тобто 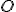 – центр основи конуса, а відрізки
– центр основи конуса, а відрізки 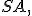
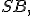
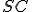 – твірні конуса,
– твірні конуса, 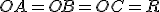 , де
, де 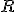 – радіус основи конуса.
– радіус основи конуса.
Відомо, що для рівностороннього трикутника виконується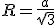 (1)
(1)
Розглянемо прямокутний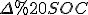 :
:
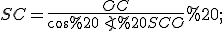
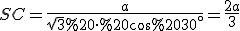 (2)
(2)
Бічну поверхню конуса обчислимо за формулою
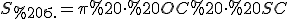 .
.
З рівностей (1) та (2), маємо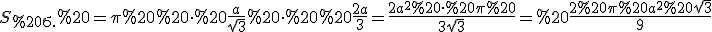 .
.
Відповідь: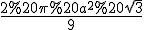 .
.
№2. В основі піраміди лежить рівнобедрений трикутник, бічна сторона якого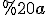 , а кут при основі
, а кут при основі 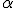 . Бічні грані нахилено до основи під кутом
. Бічні грані нахилено до основи під кутом 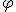 . Знайти площу бічної поверхні вписаного в піраміду конуса.
. Знайти площу бічної поверхні вписаного в піраміду конуса.
Розв’язання.
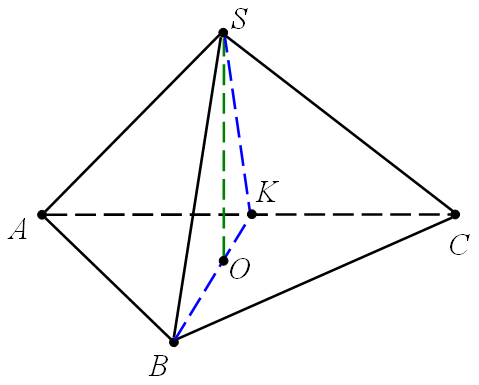
Нехай в основі піраміди лежить рівнобедрений трикутник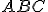 , в якому
, в якому 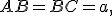
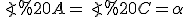 .
.
Опустимо з вершини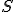 перпендикуляр
перпендикуляр 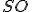 на площину основи піраміди та вписаного конуса.
на площину основи піраміди та вписаного конуса.
Побудуємо кут нахилу бічної грані до основи. Проведемо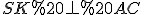 , тоді за теоремою про три перпендикуляри
, тоді за теоремою про три перпендикуляри 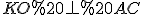 , отже за означенням
, отже за означенням 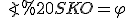 .
.
Нехай навколко піраміди
Оскільки всі ребра піраміди рівно нахилені до площини основи, то
точка
Відомо, що для рівностороннього трикутника виконується
Розглянемо прямокутний
Бічну поверхню конуса обчислимо за формулою
З рівностей (1) та (2), маємо
Відповідь:
№2. В основі піраміди лежить рівнобедрений трикутник, бічна сторона якого
Розв’язання.
Нехай в основі піраміди лежить рівнобедрений трикутник
Опустимо з вершини
Побудуємо кут нахилу бічної грані до основи. Проведемо

Оскільки всі бічні грані піраміди рівнонахилені до основи, то точка 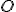 є центром вписаного кола в
є центром вписаного кола в 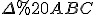 , тобто центром основи конуса,
, тобто центром основи конуса, 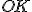 – радіус основи конуса,
– радіус основи конуса, 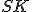 – твірна конуса.
– твірна конуса.
Розглянемо основу піраміди.
З прямокутного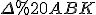 знайдемо
знайдемо 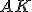 :
:
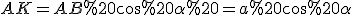 .
.
Оскільки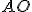 – бісектриса
– бісектриса 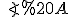 (т.
(т. 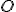 – точка перетину бісектрис
– точка перетину бісектрис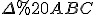 ), то
), то 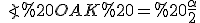 , то
, то
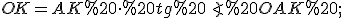
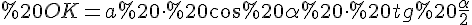 (1)
(1)
З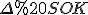 маємо
маємо 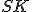 :
: 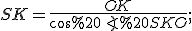
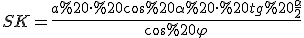 (2)
(2)
Площа бічної поверхні конуса з (1) та (2)
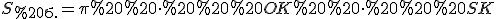 ,
,
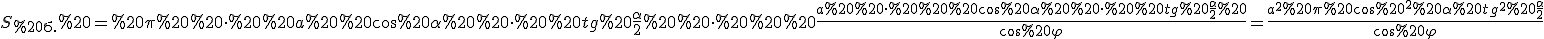 .
.
Відповідь: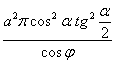 .
.
Тренувальні вправи
№1. У правильній трикутній піраміді основи дорівнюють , а плоский кут при вершині
, а плоский кут при вершині 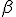 . Визначити площу бічної поверхні конуса, вписаного в піраміду.
. Визначити площу бічної поверхні конуса, вписаного в піраміду.
Відповідь до завдання: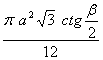 .
.
№2. У правильній трикутній піраміді плоский кут при вершині дорівнює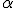 . Знайти повну поверхню вписаного конуса, якщо площа основи піраміди
. Знайти повну поверхню вписаного конуса, якщо площа основи піраміди 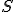 .
.
Відповідь до завдання: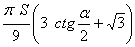 .
.
№3. У правильній чотирикутній піраміді плоский кут при вершині дорівнює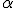 . Визначити площу бічної поверхні конуса, описаного навколо піраміди, якщо її висота
. Визначити площу бічної поверхні конуса, описаного навколо піраміди, якщо її висота 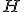 .
.
Відповідь до завдання: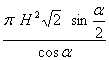
№4. В конус вписано піраміду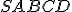 , основою якої є трапеція
, основою якої є трапеція 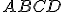 . Відомо, що
. Відомо, що 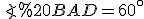 ,
, 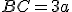 ,
, 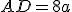 (
(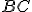 і
і 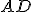 – основи трапеції), висота
– основи трапеції), висота 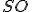 піраміди
піраміди 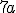 . Знайти площу бічної поверхні конуса.
. Знайти площу бічної поверхні конуса.
Відповідь до завдання: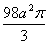 .
.
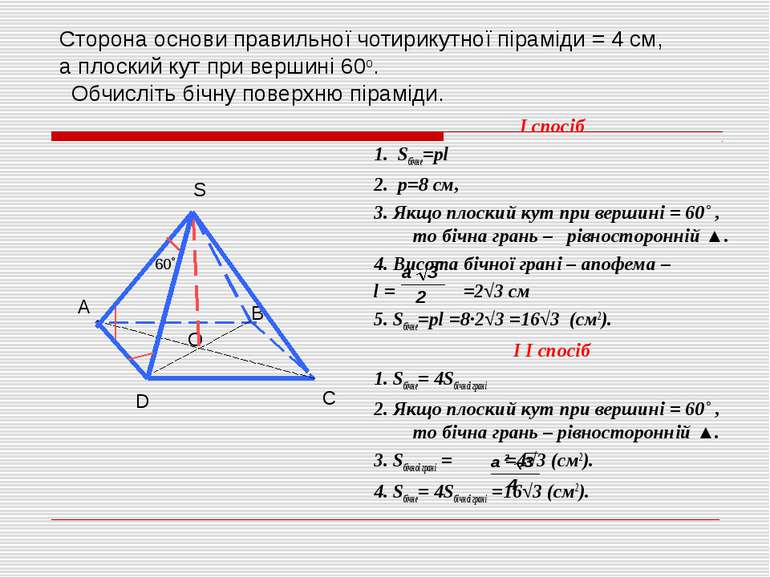
Для довідки:
Розглянемо основу піраміди.
З прямокутного
Оскільки
З
Площа бічної поверхні конуса з (1) та (2)
Відповідь:
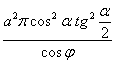 .
.Тренувальні вправи
№1. У правильній трикутній піраміді основи дорівнюють
Відповідь до завдання:
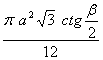 .
.№2. У правильній трикутній піраміді плоский кут при вершині дорівнює
Відповідь до завдання:
№3. У правильній чотирикутній піраміді плоский кут при вершині дорівнює
Відповідь до завдання:
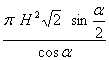
№4. В конус вписано піраміду
Відповідь до завдання:

Для довідки:

Немає коментарів:
Дописати коментар