Модулем додатного числа називається саме це число, модулем від'ємного числа називається число, протилежне даному, модуль нуля дорівнює нулю.
Модуль числа α позначається символом |а| і читається «модуль числа а».
Згідно з означенням:
Згідно з означенням:
Виконання вправ
1. Знайдіть модулі чисел:
а) -; б) -1; в) 1- ; г) 2- ()2.
Відповідь: а) ; б) -1; в) -1; г) 0.
2. Запишіть вирази без знака модуля:
а) ; б) ; в) ; г) .
Відповідь: а) 2-; б)-1; в) sin 3; г) lg 5.
3. Запишіть вирази, без знака модуля:
а) х + ; б) - х; в) х - ; г) .
Відповідь: а) б) в) г)
Геометричний зміст модуля:
числа є відстань від початку координат до точки,
що зображає дане число (рис. 1) на координатній прямій.
Дійсно, якщо а > 0, то відстань ОА дорівнює а.
Якщо b < 0, то відстань 0В дорівнює -b.
числа є відстань від початку координат до точки,
що зображає дане число (рис. 1) на координатній прямій.
Дійсно, якщо а > 0, то відстань ОА дорівнює а.
Якщо b < 0, то відстань 0В дорівнює -b.
Теорема Модуль різниці двох чисел дорівнює відстані між точками,
які є зображеннями чисел на координатній прямій.
які є зображеннями чисел на координатній прямій.
Доведення
Візьмемо числа a і b. Позначимо на координатній прямій числа а, b,
а — b через А, В, С (рис. 2). При паралельному перенесенні
вздовж осі х на b, точка О перейде в точку В, а точка С — в точку А,
тобто ОС=АВ. Оскільки за означенням модуля ОС=, то АВ= ,
що і треба було довести.
а — b через А, В, С (рис. 2). При паралельному перенесенні
вздовж осі х на b, точка О перейде в точку В, а точка С — в точку А,
тобто ОС=АВ. Оскільки за означенням модуля ОС=, то АВ= ,
що і треба було довести.
Прості рівняння і нерівності з модулем зручно розв'язувати
використовуючи геометричний зміст модуля. Розглянемо приклади.
використовуючи геометричний зміст модуля. Розглянемо приклади.
Приклад 1. Розв'яжіть рівняння |х| = 5.
Розв'язання
Співвідношення |х| = 5 геометричне означає, що відстань від точки х
до початку координат дорівнює 5, тобто х = 5 або х = -5. Відповідь: ±5.
до початку координат дорівнює 5, тобто х = 5 або х = -5. Відповідь: ±5.
Приклад 2. Розв'яжіть рівняння |х + 3| = 2.
Розв'язання
Перепишемо співвідношення |х + 3| = 2 у вигляді |х - (-3)| = 2,
яке геометрична означає, що відстань від точки -3 до точки х дорівнює 2.
Відклавши від точки -3 на координатній прямій відрізок довжиною 2
(вправо і вліво), одержимо х = -1 або х = -5.
яке геометрична означає, що відстань від точки -3 до точки х дорівнює 2.
Відклавши від точки -3 на координатній прямій відрізок довжиною 2
(вправо і вліво), одержимо х = -1 або х = -5.
Відповідь: -1; -5.
Приклад 3. Розв'яжіть нерівність |х - 3| < 2.
Розв'язання
Розв'язати нерівність |х - 3| < 2 геометричне означає: знайти точки х,
відстань від яких до точки 3 не перевищує 2. На відстані 2 від точки З
знаходяться точки 1 і 5 (рис. 3). Отже, 1 х 5.
відстань від яких до точки 3 не перевищує 2. На відстані 2 від точки З
знаходяться точки 1 і 5 (рис. 3). Отже, 1 х 5.
Відповідь: 1 х 5.
Приклад 4. Розв'яжіть нерівність |2х + 1| 3 .
Розв'язання
Перепишемо нерівність |2х + 1| 3 у вигляді |2х – (- 1)| 3 ,
яка геометрично означає, що відстань від точки 2х до точки -1
не менша 3 (рис. 4). На відстані 3 від точки -1 знаходяться точки 2 і - 4.
Таким чином, 2х 2 або 2х - 4,
яка геометрично означає, що відстань від точки 2х до точки -1
не менша 3 (рис. 4). На відстані 3 від точки -1 знаходяться точки 2 і - 4.
Таким чином, 2х 2 або 2х - 4,
звідси х 1 або х -2.
Відповідь: х 1 або х -2.
Виконання вправ
1. Розв'яжіть рівняння:
а) |х – 1| = 2; б) |х + 3| = 1; в) |2х + 1| = 3; г) |2х – 3| = 9.
Відповідь: а) -1; 3; б) -2; -4; в) 1; -2; г) -3; 6.
2. Розв'яжіть нерівності:
а) |х + 2| > 2; б) |2 – х| > 3; в) |2х – 3| < 5; г) |1 + 2х| < 1.
Відповідь: а) х < -4 або х > 0; б) х < -1 або х > 5; в) -1 < х < 4; г) -1 < х < 0.
3. Множину чисел, зображених на рис. 5, запишіть у вигляді нерівності,
що містить знак модуля.
що містить знак модуля.
Відповідь: а) |х| < 1; б) |х| < 2; в) |х – 3| < 3; г) |х + 2| < 2.
4. Множину чисел, зображених на рис. 6, запишіть у вигляді нерівності,
що містить знак модуля.
що містить знак модуля.
Відповідь: а) |х| 1; б) |х| > 3; в) |х + 2| 1; г) |х + 4| > 1.
5. Розв'яжіть рівняння:
а) ||х| – 1| = 2; б) ||х| – 4| = 1; в) ||х – 1| – 1| = 2; г) ||х + 1| + 1| = 2.
Відповідь: а) ±3; б) ±3; ±5; в) -2; 4; г) 0; -2.
6. Розв'яжіть нерівність:
а) ||х| - 2| 1; б) ||х| - 5| 2; в) ||х + 1| + 1| 3.
Відповідь: а) -3 х -1 або 1 х 3; б) -7 х -3 або 3 х 7; в) -3 х 1.
Використовуючи означення та геометричний зміст модуля дійсного числа,
можна сформулювати такі його властивості.
можна сформулювати такі його властивості.
1. Модуль дійсного числа — невід’ємне число, тобто |а| 0.
2. Модулі протилежних чисел рівні: |а| =|-а|.
3. Модуль добутку дорівнює добутку модулів множників: |аb| = |а · b|.
Дійсно, якщо а і b — числа однакових знаків, то ab > 0 і |аb| = |а| · |b|.
Якщо α і b — числа, які мають різні знаки, то ab < 0 і |аb| = = -ab.
З другого боку |а|·|b| = - ab. Отже, |аb| = |а|•|b|.
З другого боку |а|·|b| = - ab. Отже, |аb| = |а|•|b|.
4. Квадрат модуля числа дорівнює квадрату числа: |а|2 = а2.
5. Модуль дробу дорівнює модулю чисельника, поділеному на модуль
знаменника (якщо. модуль знаменника не дорівнює нулю):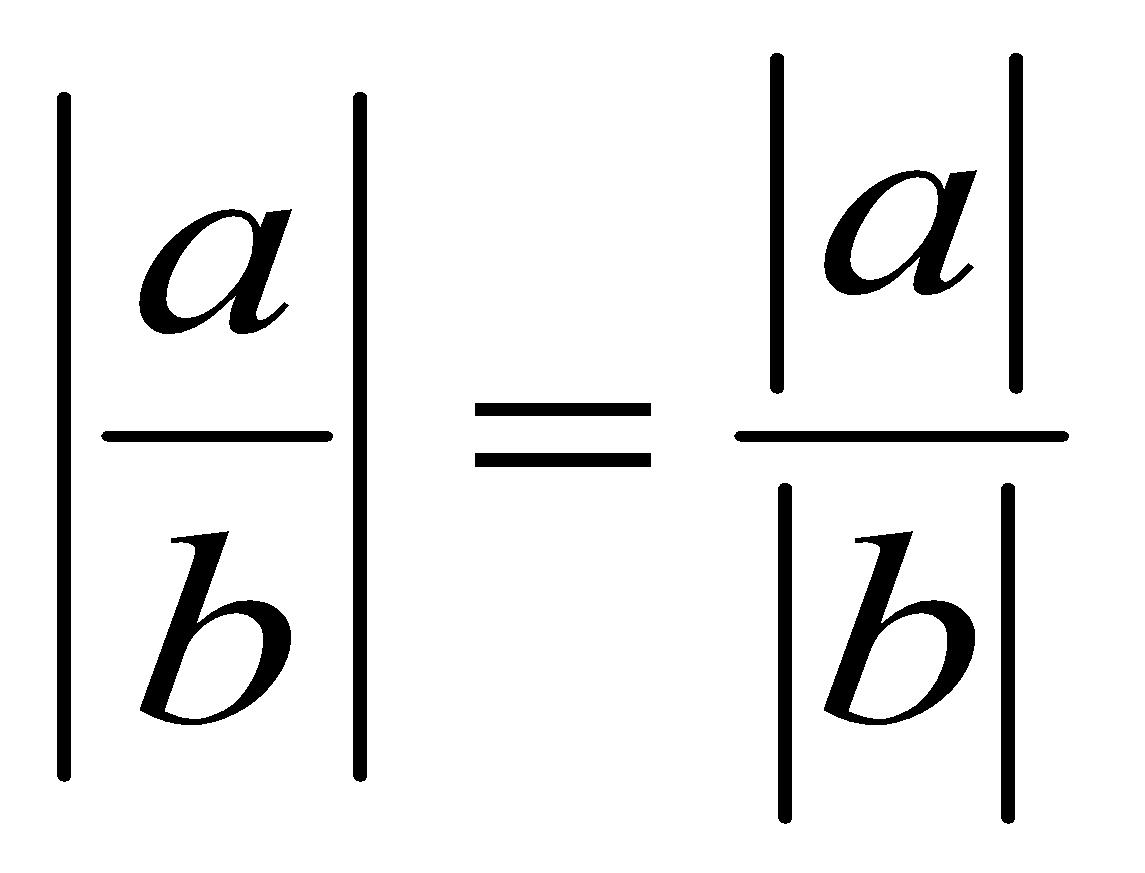
Дійсно, оскільки а = ·b, то за властивістю 3 маємо: ,
звідки .
знаменника (якщо. модуль знаменника не дорівнює нулю):
Дійсно, оскільки а = ·b, то за властивістю 3 маємо: ,
звідки .
6. Модуль суми не перевищує суми модулів доданків: |а + b| |a| +|b|.
Оскільки -|a|  а
а  |a| і -|b|
|a| і -|b|  b
b  |b|, то, додавши почленно ці нерівності, одержимо
|b|, то, додавши почленно ці нерівності, одержимо
-|а| - |b|  а + b
а + b  |а| + |b|, або
|а| + |b|, або
-(|а| + |b|) а + b |а| + |b|,
що означає |a + b| |а| + |b|.
Рівняння з модулями
1. Рівняння |f(x)| = | g(x)| рівносильне об'єднанню рівнянь:
f(x) = g(x) та f(x) = -g(x).
Приклад. Розв'яжіть рівняння: |х|= |4 - х|.
Розв'язання
Рівняння |х| = |4 - х| рівносильне рівнянням x = 4 - x та x = -4 + x. Тоді
1) x = 4 - x; 2x = 4; x = 2.
2) x = - 4 + x; Οx = -4; розв'язків немає.
Відповідь: 2.
2. Рівняння |f(x)| = g(x) рівносильне двом системам:
та
Приклад. Розв'яжіть рівняння |х2 – х – 8| = – х.
Розв'язання
Рівняння |х2 – х – 8| = – х рівносильне системам
Відповідь: -2; 2.
3. Приклад. Розв'яжіть рівняння |х + 1| + |х – 2| = 3.
Розв'язання
Вирази х + 1 і х – 2 дорівнюють нулю відповідно при
х = – 1 і х = 2. Тому розглянемо такі три випадки (рис. 7).
І) Знайдемо всі розв'язки рівняння, які задовольняють умову х – 1.
– 1.
Якщо х –1, то х + 1 0, х – 2 0 і дане рівняння має вигляд:
- х - 1 - х + 2 = 3; -2х + 1 = 3; -2х = 2; х = -1.
II) Якщо -1 < х  2, то |х + 1| = х + 1, |х – 2| = – х + 2 і дане рівняння
2, то |х + 1| = х + 1, |х – 2| = – х + 2 і дане рівняння
набирає вигляду: х + 1 – х + 2 = 3; 0х +3 = 3; 0х = 0.
Розв'язком цього рівняння є довільне число з проміжку -1 < х < 2.
набирає вигляду: х + 1 – х + 2 = 3; 0х +3 = 3; 0х = 0.
Розв'язком цього рівняння є довільне число з проміжку -1 < х < 2.
IІІ) Якщо х > 2, то |х + 1| = х + 1, |х – 2| = х – 2 і дане рівняння набирає вигляду:
х + 1 + х – 2 = 3; 2х – 1 = 3; 2х = 4; х = 2 — не входить в проміжок х > 2.
Отже, дане рівняння має корені -1  х
х  2.
2.
Відповідь: -1 х 2.
Нерівності з модулем
- Нерівність |f(x)| < g(x) рівносильна системі
- або подвійній нерівності - g(x) < f(x) < g(x).
Приклад. Розв'яжіть нерівність |х2 + 5x| < 6.
Розв'язання:
Нерівність |х2 + 5х| < 6 рівносильна подвійній нерівності – 6 < х2 + 5x < 6, тобто системі
Відповідь: (-6; - 3) (-2; 1).
2. Нерівність |f(x)| > g(x) рівносильна двом нерівностям: f(x) > g(x) та f(x) < -g(x).
Приклад. Розв'яжіть нерівність |3х - 2| > 2х + 1.
Розв'язання
Нерівність |3х - 2| > 2х + 1 рівносильна об'єднанню двох нерівностей:
3х - 2 > 2х + 1 та 3х - 2 < - 2х - 1.
1) 3х - 2 > 2х + 1; х > 3.
2) 3х - 2 < -2х - 1; 5х < 1; х < .
Отже, дана нерівність має розв'язок х е .
Відповідь: .
3. Нерівність |f(x)| > |g(x)| рівносильна нерівності f2(x) > g2(x}·
Приклад. Розв'яжіть нерівність |3 + x| |x|.
Розв'язання
|3 + х| |х|; (3 + х)2 х2; 9 + 6х + х2 х2; 6х -9; х ; х -1,5.
Відповідь: [-1,5; +).
4. Приклад. Розв'яжіть нерівність |х – 1| + |х - 2| > х + 3.
Розв'язання
Ця нерівність рівносильна трьом системам:
Відповідь: x (-; 0) U (6; +).
Модуль дійсного числа

Немає коментарів:
Дописати коментар