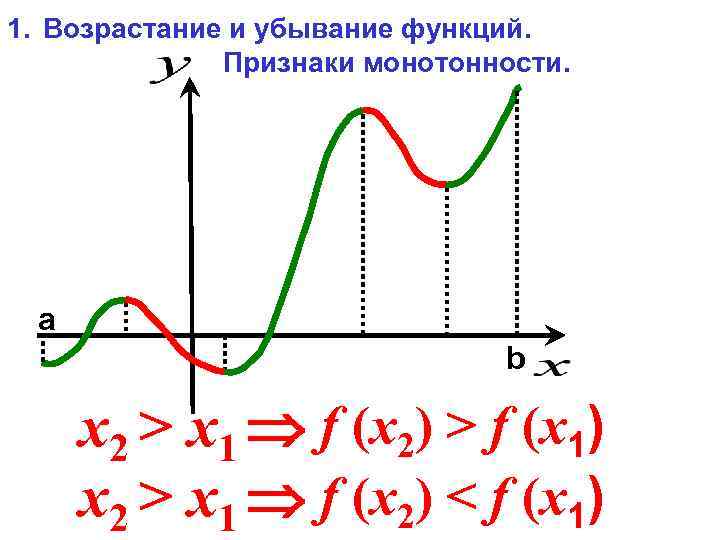
Монотонність функції
Функція  називається зростаючою на даному числовому проміжку Х, якщо більшому значенню аргументу
називається зростаючою на даному числовому проміжку Х, якщо більшому значенню аргументу  відповідає більше значення функції
відповідає більше значення функції  , тобто для будь-яких
, тобто для будь-яких 
 з
з 


Функція
 називається спадною на даному числовому проміжку Х, якщо більшому значенню аргументу
називається спадною на даному числовому проміжку Х, якщо більшому значенню аргументу  відповідає менше значення функції
відповідає менше значення функції  , тобто для будь-яких
, тобто для будь-яких 
 з
з 



Функція, тільки зростаюча або тільки спадна на даному числовому проміжку, називається монотонною на цьому проміжку.
Прикладами монотонно зростаючих функцій є:
 ,
,  ,
,  .
.
Прикладами монотонно спадних –  ,
,  ,
,  .
.
 ,
,  ,
,  .
.
А, наприклад, функція  не є монотонною на всій області визначення, оскільки при
не є монотонною на всій області визначення, оскільки при

 вона є спадною, а при
вона є спадною, а при 
 – зростаючою.
– зростаючою.
Приклад 1. Дослідити на монотонність функцію:
а) ;
;
б) ,
, 
 .
.
Розв’язання
а) Функція зростає на всій області визначення. Дійсно,
зростає на всій області визначення. Дійсно, 
 . Нехай
. Нехай  , тоді
, тоді  , отже
, отже  .
.
б) Функція ,
, 
 спадає. Дійсно, нехай
спадає. Дійсно, нехай  . Маємо
. Маємо

 , отже,
, отже,  .
.
Проміжки знакосталості і нулі функції
 не є монотонною на всій області визначення, оскільки при
не є монотонною на всій області визначення, оскільки при
 вона є спадною, а при
вона є спадною, а при 
 – зростаючою.
– зростаючою.Приклад 1. Дослідити на монотонність функцію:
а)
 ;
;б)
 ,
, 
 .
.Розв’язання
а) Функція
 зростає на всій області визначення. Дійсно,
зростає на всій області визначення. Дійсно, 
 . Нехай
. Нехай  , тоді
, тоді  , отже
, отже  .
.б) Функція
 ,
, 
 спадає. Дійсно, нехай
спадає. Дійсно, нехай  . Маємо
. Маємо
 , отже,
, отже,  .
.Проміжки знакосталості і нулі функції
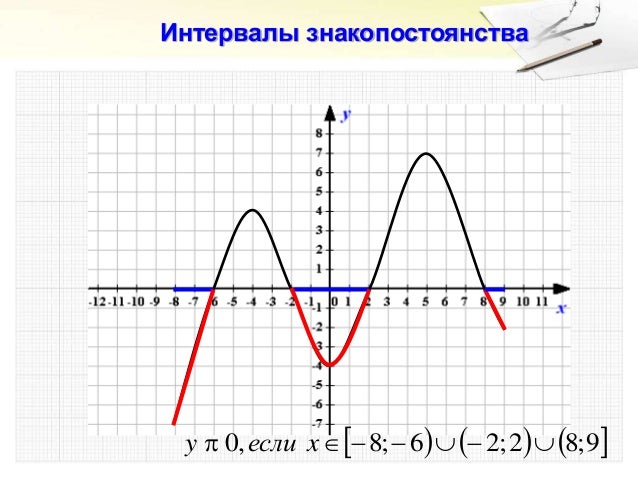 Числові проміжки, на яких функція зберігає свій знак (тобто залишається додатною або від’ємною), називаються проміжками знакосталості функції.
Числові проміжки, на яких функція зберігає свій знак (тобто залишається додатною або від’ємною), називаються проміжками знакосталості функції.
Наприклад, для функції  ,
,  при
при  і
і  при
при  .
.
Значення аргументу , при яких функція
, при яких функція  , називаються нулями (або коренями) функції. Зрозуміло, що значення аргументу, при яких функція перетворюється в нуль, – це абсциси точок перетину графіка функції з віссю 0х.
, називаються нулями (або коренями) функції. Зрозуміло, що значення аргументу, при яких функція перетворюється в нуль, – це абсциси точок перетину графіка функції з віссю 0х.
Лінійна функція, її властивості
 ,
,  при
при  і
і  при
при  .
.Значення аргументу
 , при яких функція
, при яких функція  , називаються нулями (або коренями) функції. Зрозуміло, що значення аргументу, при яких функція перетворюється в нуль, – це абсциси точок перетину графіка функції з віссю 0х.
, називаються нулями (або коренями) функції. Зрозуміло, що значення аргументу, при яких функція перетворюється в нуль, – це абсциси точок перетину графіка функції з віссю 0х.Лінійна функція, її властивості
Функція, задана формулою  , де k і b – дійсні числа, називається лінійною.
, де k і b – дійсні числа, називається лінійною.
Основні властивості функції
1. , тобто вираз
, тобто вираз  має зміст при будь-якому значенні х.
має зміст при будь-якому значенні х.
2. .
.
3. Функція є функцією загального виду, тобто не є ні парною, ні непарною. Замінимо
є функцією загального виду, тобто не є ні парною, ні непарною. Замінимо  на
на  :
:  , тобто
, тобто  . Як видно,
. Як видно,  та
та  .
.
4. При функція
функція  приймає вигляд
приймає вигляд  і називається прямою пропорційністю. Число
і називається прямою пропорційністю. Число  називається коефіцієнтом пропорційності. Пряма пропорційність характеризується властивістю: «із збільшенням (зменшенням) значення х в декілька разів відповідне значення
називається коефіцієнтом пропорційності. Пряма пропорційність характеризується властивістю: «із збільшенням (зменшенням) значення х в декілька разів відповідне значення  збільшується (зменшується) у стільки ж разів», тобто
збільшується (зменшується) у стільки ж разів», тобто  .
.
Функція є непарною. Її графік проходить через точку
є непарною. Її графік проходить через точку  і являє собою пряму лінію.
і являє собою пряму лінію.
5. Графік лінійної функції може бути отриманий з графіка функції
може бути отриманий з графіка функції  паралельним перенесенням останнього на
паралельним перенесенням останнього на  одиниць вздовж осі 0y. І оскільки графіком
одиниць вздовж осі 0y. І оскільки графіком  є пряма, то і графік функції
є пряма, то і графік функції  є пряма лінія. Вона перетинає вісь 0y в точці
є пряма лінія. Вона перетинає вісь 0y в точці  , і нахилена до осі 0х під кутом
, і нахилена до осі 0х під кутом  , тангенс якого дорівнює
, тангенс якого дорівнює  , тобто
, тобто  . Якщо
. Якщо  , то
, то  – гострий кут, якщо
– гострий кут, якщо  , то
, то  – тупий кут (рис. 4).
– тупий кут (рис. 4).

 , де k і b – дійсні числа, називається лінійною.
, де k і b – дійсні числа, називається лінійною.Основні властивості функції

1.
 , тобто вираз
, тобто вираз  має зміст при будь-якому значенні х.
має зміст при будь-якому значенні х.2.
 .
.3. Функція
 є функцією загального виду, тобто не є ні парною, ні непарною. Замінимо
є функцією загального виду, тобто не є ні парною, ні непарною. Замінимо  на
на  :
:  , тобто
, тобто  . Як видно,
. Як видно,  та
та  .
.4. При
 функція
функція  приймає вигляд
приймає вигляд  і називається прямою пропорційністю. Число
і називається прямою пропорційністю. Число  називається коефіцієнтом пропорційності. Пряма пропорційність характеризується властивістю: «із збільшенням (зменшенням) значення х в декілька разів відповідне значення
називається коефіцієнтом пропорційності. Пряма пропорційність характеризується властивістю: «із збільшенням (зменшенням) значення х в декілька разів відповідне значення  збільшується (зменшується) у стільки ж разів», тобто
збільшується (зменшується) у стільки ж разів», тобто  .
.Функція
 є непарною. Її графік проходить через точку
є непарною. Її графік проходить через точку  і являє собою пряму лінію.
і являє собою пряму лінію.5. Графік лінійної функції
 може бути отриманий з графіка функції
може бути отриманий з графіка функції  паралельним перенесенням останнього на
паралельним перенесенням останнього на  одиниць вздовж осі 0y. І оскільки графіком
одиниць вздовж осі 0y. І оскільки графіком  є пряма, то і графік функції
є пряма, то і графік функції  є пряма лінія. Вона перетинає вісь 0y в точці
є пряма лінія. Вона перетинає вісь 0y в точці  , і нахилена до осі 0х під кутом
, і нахилена до осі 0х під кутом  , тангенс якого дорівнює
, тангенс якого дорівнює  , тобто
, тобто  . Якщо
. Якщо  , то
, то  – гострий кут, якщо
– гострий кут, якщо  , то
, то  – тупий кут (рис. 4).
– тупий кут (рис. 4).

Немає коментарів:
Дописати коментар