Усе про рівнобічну трапецію

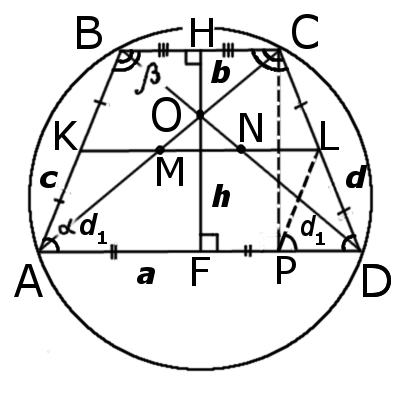
Ознаки рівнобічної трапеції

Трапеція буде рівнобічною, якщо виконується одна із цих умов:

1. Кути при основі рівні:

∠ABC = ∠BCD і ∠BAD = ∠ADC

2. Діагоналі рівні:

AC = BD

3. Однакові кути між діагоналями і основами:

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сума протилежних кутів дорівнює 180°:

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Навколо трапеції можна описати коло

Основні властивості рівнобічної трапеції

1. Сума кутів прилеглих до бокової сторони рівнобічної трапеції дорівнює 180°:

∠ABC + ∠BAD = 180° і ∠ADC + ∠BCD = 180°

2. Якщо в рівнобічну трапецію можна вписати коло, то бокова сторона дорівнює середній лінії трапеції:

AB = CD = m

3. Навколо рівнобічної трапеції можна описати коло

4. Якщо діагоналі взаємно перпендикулярні, то висота дорівнює півсумі основ (середній лінії):

h = m

5. Якщо діагоналі взаємно перпендикулярні, то площа трапеції дорівнює квадрату висоти:

S_ABCD = h²

6. Якщо в рівнобічну трапецію можна вписати коло, то квадрат висоти рівний добутку основ трапеції:

h² = BC · AD

7. Сума квадратів діагоналей дорівнює сумі квадратів бокових сторін плюс подвоєному добутку основ трапеції:

AC² + BD² = AB² + CD² + 2BC · AD

8. Пряма, що проходить через середини основ, перпендикулярна основам і являється віссю симетрії трапеції:

HF ┴ BC ┴ AD

9. Висота (CP), опущена із вершини (C) на більшу основу (AD), ділить її на більший відрізок (AP), який дорівнює півсумі основ та менший (PD) - дорівнює піврізниці основ:

AP =	BC + AD
	2

PD =	AD - BC
	2

10. Також дивіться властивості трапеції

Сторони рівнобічної трапеції

Формули довжин сторін рівнобічної трапеції:

1. Формули довжин сторін через інші сторони, висоту та кут:

a = b + 2h ctg α = b + 2c cos α

b = a - 2h ctg α = a - 2c cos α

c =	h	=	a - b
	sin α		2 cos α

2. Формула довжини сторін трапеції через діагоналі та інші сторони:

a =	d12 - c2	b =	d12 - c2	c = √d12 - ab
	b		a

3. Формули довжини основ через площу, висоту та іншу основу:

a =	2S	- b      b =	2S	- a
	h		h

4. Формули довжини бокової сторони через площу, середню лінію та кут при основі:

с =	S
	m sin α

5. Формули довжини бокової сторони через площу, основи та кут при основі:

с =	2S
	(a + b) sin α

Середня лінія рівнобічної трапеції

Формули довжини середньої лінії рівнобічної трапеції:

1. Формула визначення довжини середньої лінії через основи, висоту та кут при основі:

m = a - h ctg α = b + h ctg α = a - √c² - h² = b + √c² - h²

2. Формула середньої лінії трапеції через площу та сторону:

m =	S
	c sin α

Висота рівнобічної трапеції

Формули визначення довжини висоти рівнобічної трапеції:

1. Формула висоти через сторони:

h =	1	√4c2 - (a - b)2
	2

2. Формула висоти через сторони та кут прилеглий до основи:

h =	a - b	tg β	= c sin β
	2

Діагоналі рівнобічної трапеції

Діагоналі рівнобічної трапеції рівні:

d₁ = d₂

Формула довжини діагоналей рівнобічної трапеції:

1. Формула довжини діагоналі через сторони:

d₁ = √с² + ab

2. Формули довжини діагоналі по теоремі косинусів:

d₁ = √a² + c² - 2ac cos α

d₁ = √b² + c² - 2bc cos β

3. Формула довжини діагоналі через висоту та середню лінію:

d₁ = √h² + m²

4. Формула довжини діагоналі через висоту та основи:

d1 =	1	√4h2 + (a + b)2
	2

Площа рівнобічної трапеції

Формули площі рівнобічної трапеції:

1. Формула площі через сторони:

S =	a + b	√4c2 - (a - b)2
	4

2. Формула площі через сторони та кут:

S = (b + c cos α) c sin α = (a - c cos α) c sin α

3. Формула площі через радіус вписаного кола та кут між основою та боковою стороною:

S =	4 r 2	=	4 r 2
	sin α		sin β

4. Формула площі через основи та кут між основою та боковою стороною:

S =	ab	=	ab
	sin α		sin β

5. Формула площі рівнобічної трапеції, в яку можна вписати коло:

S = (a + b) · r = √ab·c = √ab·m

6. Формула площі через діагоналі та кут між ними:

S =	d12	· sin γ	=	d12	· sin δ
	2			2

7. Формула площі через середню лінію, бокову сторону та кут при основі:

S = mc sin α = mc sin β

8. Формула площі через основи та висоту:

S =	a + b	· h
	2

Коло описане навколо трапеції

Коло можна описати лише навколо рівнобічної трапеції!!!

Формула радіуса описаного навколо трапеції кола:

1. Формула радіуса через сторони та діагональ:

R =	a·c·d1
	4√p(p - a)(p - c)(p - d1)

де

p =	a + c + d1
	2

a - більша основа

Джерело